Vamos a machacar algunos números sobre estos hilos. Como ejemplo:
Eso si , para los que padezcan con las fórmulas, ecuaciones y matemáticas a cascoporro, mejor no seguir leyendo....
Un esquema de un tramo de longitud L de dicho hilo:
- En número de espiras de kanthal será
- La sección del hilo de níquel es
- Un espira de kanthal tiene espesor dK y se
arrolla sobre un diámetro dN+dK/2 , y su
longitud es
así que la longitud total de kanthal arrollado será:
- La sección del kanthal es
Unos datos más que nos harán falta:
Resistividad del
kanthal A-1
|
ρK =
1,45.10-6 Ωm
|
Resistividad del
níquel
|
ρN = 0,07.10-6
Ωm
|
Así que en un tramo de clapton de longitud L:
- Tendremos L de níquel con resistencia
[Ec.1] - Una longitud LK de kanthal con resistencia
El arrollamiento de kanthal sobre el níquel es,
conceptualmente, un conjunto de dos resistencias, una de níquel y
otra de kanthal, en paralelo. Da igual que consideremos una espira,
todas, varias, incluso un corte infinitesimal, cada porción suma a
las siguientes pues están en serie, así que aunque kanthal y níquel
se tocas constantemente, para el cálculo de la resistencia final da
igual que consideremos la hélice de kanthal separada del níquel, y
cada resistencia sumada en paralelo. (Es la continuidad de cablesconductores).
Para dos resistencia en paralelo, la resistencia
final R cumple:
luego
¡pero en [Ec.1] eso mismo nos daba RN!
Como cabría esperar con la gran diferencia de resistividades, una
sección cuatro veces menor (mitad de diámetro) y una longitud mucho
mayor, la resistencia de kanthal es muy superior y al ponerla en
paralelo el conjunto tienen una resistencia sensiblemente similar a
la del núcleo de níquel. Esto puede extrapolarse para claptons en
los que ambos materiales tienen igual resistividad.
Por ejemplo,
si nuestro caso fuera con ambos hilos de kanthal,
en un tramo de clapton de
longitud L:
- Tendremos L de kanthal con resistencia
- La misma longitud LK de kanthal con resistencia
¡de nuevo el mismo valor
de RN!
La
resistencia de un clapton es sensiblemente igual a la de su núcleo,
el arrollamiento en paralelo apenas aporta resistencia, lo que aporta
es capacidad calorífica, superficie de intercambio de calor y
capacidad de retener líquido por capilaridad.
Y podríamos extender este resultado a todo hilo complejo en el que
haya una sección importante y otra menor y por arrollamiento, mucho
más larga.
Pero
nuestro clapton lleva un núcleo de níquel, que aparte de ser menos
resistivo, tiene una marcada variación de resistividad con el
aumento de temperatura. ¿La constante temperature
coefficient for resistance,
TCR, usada en los mods en modo TC, se verá afectada por esta
agrupación?
Por
el mismo argumento de las resistencia en paralelo, aunque la de
kanthal no varíe y la de níquel sí, ya vemos que la que importa es
la de níquel, pero para escépticos, vamos a seguir calculando el
TCR aparente de la combinación. Para ello recordaremos que:
siendo
R la resistencia a la temperatura de trabajo, R0 la de
calibración, “fijada” supuesta a 20 ºC, y T, T0
dichas temperaturas. Vamos a calcular las resistencias a 20 ºC y a
220 ºC del conjunto de longitud L. Para generalizar a
todo tipo de materiales, vamos a introducir un parámetro:
la relación entre la resistencia del arrollamiento y la del
núcleo....
...que
en nuestro caso vale más de dos millones, o sea 2,5.106....y
calculamos....
T – T0 = 200 K
(de 20ºC a 220ºC); a 220 ºC:
RN
= RN0 [1 + TCRN (T – T0)]; RK
= RK0 (al kanthal no le varía la resistividad con la
temperatura).
recordando
que para el níquel TCR = 0,00575 K-1....
La resistencia final del tramo de clapton de
longitud L, recordando que kanthal y níquel están en paralelo:
- A 20 ºC,
- A 220 ºC,
Luego pasamos de
a 20 ºC, a
a 220ºC.....¿que TCR “aparente” hay?
Llamando a dicho “TCR aparente” TCR*,
[Ec. 2]
pero K hemos visto que es muy grande, K>30000
para núcleo y arrollamiento exterior ambos de kanthal, y mayor de un
millón para núcleo de níquel y arrollamiento de kanthal.....
… en tal circunstancia,
y entonces...
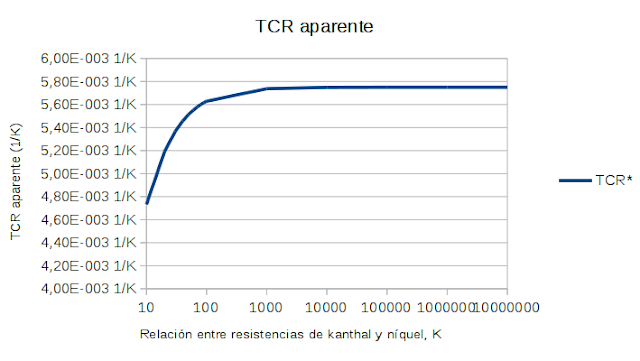
Como
puede verse, el TCR aparente se iguala al de origen para K>1000,
una relación superada para todos los clapton, alien clapton y fused
clapton habituales.....incluso cuando núcleo y exterior son de
materiales de resistividades similares: la geometría del
arrollamiento, mucho más largo y de menor sección, domina este
aspecto.
Para los que estén interesados en el documento para imprimir, lo tienen aquí.
